题目内容
已知直线l:x-y+10=0,求抛物线y2=4x上的点到直线的距离的最小值.
考点:直线与圆锥曲线的关系
专题:空间位置关系与距离
分析:设P(
,y0),利用点到直线的距离公式表示出距离,然后利用二次函数性质即可求得其最小值.
| ||
| 4 |
解答:
解:由点P在抛物线y2=4x上,设P(
,y0),
则点P到直线l:x-y+10=0的距离d=
=
,
当y0=2时d最小值为
.
所以点P到直线l:x-y+10=0的距离的最小值为
.
| ||
| 4 |
则点P到直线l:x-y+10=0的距离d=
|
| ||||
|
| (y0-2)2+36 | ||
4
|
当y0=2时d最小值为
9
| ||
| 2 |
所以点P到直线l:x-y+10=0的距离的最小值为
9
| ||
| 2 |
点评:本题考查直线与圆锥曲线的位置关系及点到直线的距离公式,考查二次函数的性质及其最值求解,解决本题关键把距离表示为二次函数,借助二次函数性质解决问题.

练习册系列答案
相关题目
已知y=f(x)为定义在R上的函数,则“存在X0∈R,使得f2(-x0)≠f2(x0)”是“f(x)为非奇非偶函数”的( )
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既不充分也不必要 |
下列函数中,与函数y=x相同的函数是( )
A、y=
| ||
B、y=
| ||
| C、y=lnex | ||
| D、y=2log2x |
 如图1,已知三棱锥的各棱长都为1,它的正视图是如图2所视的等腰三角形,则该四面体的侧视图面积为
如图1,已知三棱锥的各棱长都为1,它的正视图是如图2所视的等腰三角形,则该四面体的侧视图面积为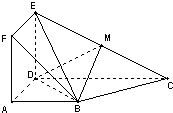 如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=
如图多面体中,正方形ADEF所在的平面与直角梯形ABCD所在的平面垂直,且AD=AB=