题目内容
设函数y=x2-4x+3,x∈[1,4],则f(x)的值域为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:先配方,求出函数的对称轴,利用二次函数的单调性即可求出.
解答:
解:∵y=x2-4x+3=(x-2)2-1,函数的对称轴x=2∈[1,4],
∴此函数在[1,4]上的最小值为:f(2)=-1,最大值为:f(4)=3,
∴函数f(x)的值域是[-1,3].
故答案为:[-1,3].
∴此函数在[1,4]上的最小值为:f(2)=-1,最大值为:f(4)=3,
∴函数f(x)的值域是[-1,3].
故答案为:[-1,3].
点评:熟练掌握二次函数的单调性是解题的关键.

练习册系列答案
相关题目
已知向量
=(1,2),
=(k+1,1),若
⊥
,则k=( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
已知a<0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) |
| B、?x∈R,f(x)≥f(x0) |
| C、?x∈R,f(x)≤f(x0) |
| D、?x∈R,f(x)≥f(x0) |
设f(x)=x2-bx+c满足y=f(x+1)是偶函数,f(0)=3,则当x≠0时,f(bx)与f(cx)的大小关系为( )
| A、f(bx)≥f(cx) |
| B、f(bx)>f(cx) |
| C、f(bx)≤f(cx) |
| D、f(bx)<f(cx) |
 由图可推得a、b、c的大小关系是( )
由图可推得a、b、c的大小关系是( )| A、c<b<a |
| B、c<a<b |
| C、a<b<c |
| D、a<c<b |
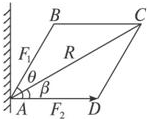 如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.
如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β. 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=