题目内容
设f(x)=x2-bx+c满足y=f(x+1)是偶函数,f(0)=3,则当x≠0时,f(bx)与f(cx)的大小关系为( )
| A、f(bx)≥f(cx) |
| B、f(bx)>f(cx) |
| C、f(bx)≤f(cx) |
| D、f(bx)<f(cx) |
考点:二次函数的性质
专题:函数的性质及应用
分析:先根据题意求得b,c的值,先讨论bx与cx,的大小,再结合二次函数的单调性即可比较f(bx)与f(cx)的大小关系即可.
解答:
解:∵y=f(x+1)是偶函数,f(x)=x2-bx+c,
∴f(1-x)=f(1+x),
得函数的对称轴是:x=1,故b=2,
可判断:函数f(x)在[1,+∞)上是增函数,在(-∞,1)上是减函数,
又f(0)=3,∴c=3,
∴bx=2x,cx=3x,
①当x>0时,3x>2x>1,f(bx)<f(cx);
②当x<0时,3x<2x<1,f(bx)<f(cx);
综上:f(bx)<f(cx).
故选:D.
∴f(1-x)=f(1+x),
得函数的对称轴是:x=1,故b=2,
可判断:函数f(x)在[1,+∞)上是增函数,在(-∞,1)上是减函数,
又f(0)=3,∴c=3,
∴bx=2x,cx=3x,
①当x>0时,3x>2x>1,f(bx)<f(cx);
②当x<0时,3x<2x<1,f(bx)<f(cx);
综上:f(bx)<f(cx).
故选:D.
点评:本小题主要考查函数单调性的应用、二次函数的性质、二次函数的性质的应用等基础知识,考查运算求解能力,考查数形结合思想、分类讨论思想.属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,若f(m)<1,则m的取值范围是( )
|
| A、(-1,1) |
| B、(-∞,1) |
| C、(-1,0] |
| D、(0,1) |
如图是函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)的图象,则其解析式是( )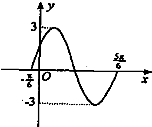
| π |
| 2 |

A、y=3sin(2x+
| ||
B、y=3sin(2x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(2x+
|
目标函数Z=2x+y,变量x,y满足
,则有( )
|
| A、Zmax=12,Zmin=3 |
| B、Zmax=12,Z无最小值 |
| C、Zmin=3,Z无最大值 |
| D、Z既无最大值,也无最小值 |
已知递增等差数列{an}中,a6=18且a2是a1,a4的等比中项,则它的第4项到第11项的和为( )
| A、180 | B、198 |
| C、189 | D、168 |