题目内容
已知a<0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) |
| B、?x∈R,f(x)≥f(x0) |
| C、?x∈R,f(x)≤f(x0) |
| D、?x∈R,f(x)≥f(x0) |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据x0满足关于x的方程2ax+b=0,x0=-
,结合二次函数的性质得出;f(x)最大值=f(-
)=f(x0),运用命题真假的判断即可得出答案.
| b |
| 2a |
| b |
| 2a |
解答:
解:∵x0满足关于x的方程2ax+b=0,
∴x0=-
,
∵a<0,函数f(x)=ax2+bx+c,
∴根据二次函数的性质∴根据命题的真假判断;D为假命题.
故选:D
∴x0=-
| b |
| 2a |
∵a<0,函数f(x)=ax2+bx+c,
∴根据二次函数的性质∴根据命题的真假判断;D为假命题.
故选:D
点评:本题考查了二次函数的性质,命题真假的判断,属于中档题,难度不大.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
要得到一个奇函数,只需将函数f(x)=sin2x-
cos2x的图象( )
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
已知函数f(x)=
,若f(m)<1,则m的取值范围是( )
|
| A、(-1,1) |
| B、(-∞,1) |
| C、(-1,0] |
| D、(0,1) |
如图是函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)的图象,则其解析式是( )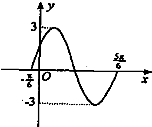
| π |
| 2 |

A、y=3sin(2x+
| ||
B、y=3sin(2x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(2x+
|
设函数f(x)=
sin2x-
cos2x,以下关于f(x)的说法正确的是( )
| ||
| 2 |
| 1 |
| 2 |
A、其图象可由 y=sin2x向右平移
| ||
B、其图象关于直线x=
| ||
C、其图象关于点(
| ||
D、在区间(-
|