题目内容
5.已知直线l1:x+ay-4=0与l2:(a-2)x+y-1=0相交于点P,若l1⊥l2,则a=1.分析 利用两条直线垂直的条件,建立方程,即可得出结论.
解答 解:∵直线l1:x+ay-4=0与l2:(a-2)x+y-1=0相交于点P,l1⊥l2,
∴a-2+a=0,∴a=1,
故答案为:1.
点评 本题考查两条直线垂直的条件,考查学生的计算能力,比较基础.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
17.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入了部分数据,如表:
(1)请将表中数据补充完整,并直接写出函数f(x)的解析式;
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[-$\frac{π}{3}$,$\frac{π}{3}$]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为($\frac{π}{12},0$),求θ的最小值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
(2)若将函数f(x)的图象上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数g(x)的图象,求当x∈[-$\frac{π}{3}$,$\frac{π}{3}$]时,函数g(x)的值域;
(3)若将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=h(x)的图象,若=h(x)图象的一个对称中心为($\frac{π}{12},0$),求θ的最小值.
14.若复数z满足(1+i)z=i(i是虚数单位),则z=( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | -$\frac{1}{2}+\frac{1}{2}i$ | C. | -$\frac{1}{2}-\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
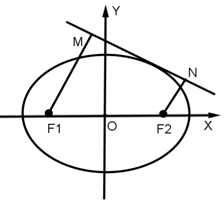 已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.
已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.