题目内容
15.已知直线l过点A(2,a),B(a,-1),且与直线m:2x-y+2=0平行.(Ⅰ)求直线l的方程;
(Ⅱ)过点A与l垂直的直线交直线m于点C,求线段BC的长.
分析 (Ⅰ)根据题意,得 $\frac{a+1}{2-a}=2$,解得a=1,即可求直线l的方程;
(Ⅱ)过点A与l垂直的直线方程为$y-1=-\frac{1}{2}(x-2)$,与直线m:2x-y+2=0联立,求出C的坐标,即可求线段BC的长.
解答 解:(Ⅰ)根据题意,得 $\frac{a+1}{2-a}=2$,解得a=1.
所以A(2,1),B(1,-1).
所求直线l的方程为2x-y-3=0.…(4分)
(Ⅱ)过点A与l垂直的直线方程为$y-1=-\frac{1}{2}(x-2)$,
整理,得x+2y-4=0.
由$\left\{{\begin{array}{l}{2x-y+2=0}\\{x+2y-4=0}\end{array}}\right.$解得C(0,2).
$|BC|=\sqrt{{{(1-0)}^2}+{{(-1-2)}^2}}=\sqrt{10}$.…(8分)
点评 本题考查直线方程,考查两点间的距离公式,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
3.己知函数 $f(x)=\frac{x-1}{x}$(其中$x∈[{\frac{1}{2},2}]$)的值域为( )
| A. | $[{-1,\frac{1}{2}}]$ | B. | [-1,2] | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},1}]$ |
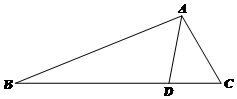 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.