题目内容
17.设函数$g(x)=({-{x^4}-{x^2}})+\frac{1}{{{e^{|x|}}-1}}$,若不等式g(x2)>g(ax)对一切x∈[-1,0)∪(0,1]恒成立,则a的取值范围是( )| A. | (-∞,-1)∪(1,+∞) | B. | (-1,1) | C. | (-1,+∞) | D. | (1,+∞) |
分析 根据函数g(x)的解析式,判断函数的奇偶性和单调性,得到关于a,x的不等式组,解出即可.
解答 解:∵$g(x)=({-{x^4}-{x^2}})+\frac{1}{{{e^{|x|}}-1}}$,
∴g(x)是偶函数,在[-1,0)递增,在(0,1]递减,
由g(x2)>g(ax)对一切x∈[-1,0)∪(0,1]恒成立,
得x2<|ax|在(0,1]恒成立,
即|a|>|x|max在(0,1]恒成立,
解得:a>1或a<-1,
故选:A.
点评 本题考查了函数的单调性、奇偶性问题,考查转化思想,是一道中档题.

练习册系列答案
相关题目
7. 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 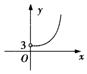 | D. |  |
9.已知命题p:?x>0,x+$\frac{4}{x}$>4,则¬p为( )
| A. | ¬p:?x≤0,x$+\frac{4}{x}$≤4 | B. | ¬p:?x≤0,x$+\frac{4}{x}$≤4 | C. | ¬p:?x>0,x$+\frac{4}{x}$≤4 | D. | ¬p:?x>0,x$+\frac{4}{x}$=4 |
6. 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )| A. | r1=r2 | B. | r1<r2 | C. | r1>r2 | D. | 无法判定 |
 已知直三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示.


