题目内容
已知点P(-1,2),圆C:(x-1)2+(y+2)2=4
(1)求过点P的圆C的切线方程,并求此切线的长度;
(2)设圆C上有两个不同的点关于直线l对称且点P到直线l的距离最长,求直线l的方程.
(1)求过点P的圆C的切线方程,并求此切线的长度;
(2)设圆C上有两个不同的点关于直线l对称且点P到直线l的距离最长,求直线l的方程.
考点:圆的切线方程
专题:计算题,直线与圆
分析:(1)设过P(-1,2)的切线为y-2=k(x+1),即kx-y+k+2=0,利用圆心到直线的距离等于半径,即可求过点P的圆C的切线方程,并求此切线的长度;
(2)确定l经过圆C的圆心C(1,-2),使P到l的距离最长,则l⊥PC,直线PC的斜率kPC=-2,可得l斜率,即可得出直线l的方程.
(2)确定l经过圆C的圆心C(1,-2),使P到l的距离最长,则l⊥PC,直线PC的斜率kPC=-2,可得l斜率,即可得出直线l的方程.
解答:
解:(1)设过P(-1,2)的切线为y-2=k(x+1),即kx-y+k+2=0
∴
=2,
∴k2+4k+4=k2+1,
∴k=-
….(2分)
两条切线l1:x=-1;l2:3x+4y-5=0….(4分)
切线长=
=4…(6分)
(2)∵圆C上有两个不同的点关于直线l对称,
∴l经过圆C的圆心C(1,-2)…(8分)
使P到l的距离最长,则l⊥PC,直线PC的斜率kPC=-2,
∴l斜率为
…..(10分)
∴直线l:y+2=
(x+1),即l方程:x-2y-3=0….(12分)
∴
| 2k+4| | ||
|
∴k2+4k+4=k2+1,
∴k=-
| 3 |
| 4 |
两条切线l1:x=-1;l2:3x+4y-5=0….(4分)
切线长=
| (-1-1)2+(2+2)2-22 |
(2)∵圆C上有两个不同的点关于直线l对称,
∴l经过圆C的圆心C(1,-2)…(8分)
使P到l的距离最长,则l⊥PC,直线PC的斜率kPC=-2,
∴l斜率为
| 1 |
| 2 |
∴直线l:y+2=
| 1 |
| 2 |
点评:本题考查直线与圆的位置关系,考查直线方程,考查学生的计算能力,比较基础.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知向量
,
满足
⊥
,|
|=1,|
|=2,则|2
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||
B、2
| ||
| C、8 | ||
| D、12 |
点A(1,3)关于直线y=kx+b的对称点是B(-2,1),则直线y=kx+b在x轴上的截距是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
甲和乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙在不同岗位服务的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若数列{an}的前n项的和Sn=3n-2,那么这个数列的通项公式为( )
A、an=(
| |||||||
B、an=an=3×(
| |||||||
| C、an=3n-2 | |||||||
D、an=
|
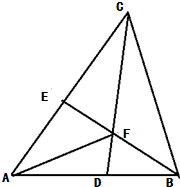 在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.
在△ABC中,∠A=60°,AB=3,AC=5,BD=1,CE=2.