题目内容
求函数的定义域.
(1)y=
(2)y=
.
(1)y=
| cosx |
(2)y=
| 1+2sinx |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:分别根据函数成立的条件,即可得到函数的定义域.
解答:
解:(1)要使函数有意义,则cosx≥0,即-
+2kπ≤x≤
+2kπ,k∈Z,
故函数的定义域为[-
+2kπ,
+2kπ],k∈Z.
(2)要使函数有意义,则1+2sinx≥0,即sinx≥-
,
即-
+2kπ≤x≤
+2kπ,k∈Z,
故函数的定义域为[-
+2kπ,
+2kπ],k∈Z.
| π |
| 2 |
| π |
| 2 |
故函数的定义域为[-
| π |
| 2 |
| π |
| 2 |
(2)要使函数有意义,则1+2sinx≥0,即sinx≥-
| 1 |
| 2 |
即-
| π |
| 6 |
| 7π |
| 6 |
故函数的定义域为[-
| π |
| 6 |
| 7π |
| 6 |
点评:本题主要考查函数定义域的求解,根据三角函数的图象和性质是解决本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知直线x-y-
=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于( )
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
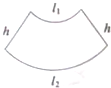 如图是一个扇环(圆环的一部分),两段圆弧的长分别为l1,l2,另外两边的长为h,先把这个扇环与梯形类比,然后根据梯形的面积公式写出这个扇环的面积并证明其正确性.参考公式:
如图是一个扇环(圆环的一部分),两段圆弧的长分别为l1,l2,另外两边的长为h,先把这个扇环与梯形类比,然后根据梯形的面积公式写出这个扇环的面积并证明其正确性.参考公式: