题目内容

证明：sin2x+sin2y-sin2x•sin2y+cos2x•cos2y=1．
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：先对sin2x和sin2x•sin2y合并同类项，利用平方关系化简，进而对cos2ysin2x+cos2x•cos2y合并同类项，化简最后利用同角三级基本关系证明结论．
解答： 证明：sin2x+sin2y-sin2x•sin2y+cos2x•cos2y=sin2x（1-sin2y）+sin2y+cos2x•cos2y=cos2ysin2x+cos2x•cos2y+sin2y=cos2y+sin2y=1，
故原等式成立．
点评：本题主要考查了同角三角函数基本关系的应用．考查了学生分析和观察能力．
练习册系列答案
相关题目
函数f（x）=2sin（
1
3
x-
π
6
）的图象为C
①图象C关于直线x=2π对称；
②f（x）在区间（-π，2π）内是增函数；
③由y=2sin
1
3
x的图象向右平移
π
6
个单位长度可以得到图象C．
以上三个诊断中，正确诊断的个数是（　　）
A、0个B、1个C、2个D、3个
已知双曲线的焦点在x轴上，一个焦点为（-
3
，0），一条渐近线为y=
2
x．
（1）求双曲线的方程
（2）过点P（1，1）能否作直线l与双曲线交于A，B两点，且P线段AB的中点，若能，求出直线l的方程，若不能，说明理由．
已知等差数列{an}的前n项和为Sn，若a1=3，Sm=15，Sm+1=24（m∈N*）．
（1）求m的值及数列{an}的通项公式；
（2）设bn=
1
Sn
，若数列{bn}的前n项和为Tn，求证：Tn＜
3
4
．
已知圆C经过点A（1，-1），B（-1，1）且圆心在直线x+y-2=0上．
（Ⅰ）求圆C的方程；
（Ⅱ）过点M（
1
2
，0）的直线l与圆C相交于E，F两点．且|EF|=2
3
，求直线l的方程．
已知函数f（x）=sin（2x+
π
6
），x∈R．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调递增区间；
（3）若x∈[0，
π
2
]，求函数f（x）的最值及其相应的x值．
求函数的定义域．
（1）y=
cosx

（2）y=
1+2sinx
．
已知数列{an}是等差数列，且a1=2，a1+a2+a3=12．
（1）求{an}的通项公式；
（2）设bn=
1
an•an+1
，求{bn}的前n项和Tn；
（3）在（2）的条件下，对任意n∈N*，Tn＞
m
23
都成立，求整数m的最大值．
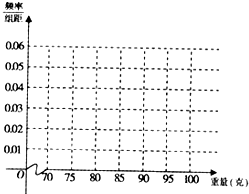从某批苹果中随机抽取100个苹果进行重量（单位：克）调查．发现重量都在70克至100克之间，结果如表：
分数（重量）[70，75）[75，80）[80，85）[85，90）[90，95）[95，100）
频数（个）5102030x10
（Ⅰ）求出表中的x值，并完成频率分布直方图；
（Ⅱ）根据频率分布直方图估计这批苹果重量的平均值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网