Question

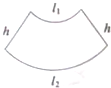如图是一个扇环（圆环的一部分），两段圆弧的长分别为l₁，l₂，另外两边的长为h，先把这个扇环与梯形类比，然后根据梯形的面积公式写出这个扇环的面积并证明其正确性．参考公式：
扇形面积公式S=

1

2

lr（l是扇形的弧长，r是扇形半径）．
弧长公式l=rα（r是扇形半径，α是扇形的圆心角）．

Answer 1

考点：类比推理

专题：推理和证明

分析：首先类比梯形的面积公式，求出扇环的面积公式；然后将扇环补成扇形，设其圆心角为θ，小扇形的半径为a，则大扇形的半径为a+h，根据扇形的面积公式以及弧长公式，证明其正确性即可．

解答： 解：梯形的面积公式为：S梯形=

(上底+下底)×高

2

将l₁、l₂类比为梯形的上、下底，h为梯形的高，
则扇环的面积为：S扇环=

(l1+l2)h

2

将扇环补成扇形，设其圆心角为θ，小扇形的半径为a，
则大扇形的半径为a+h；
∵l₁=aθ，l₂=（a+h）θ
∴a=

l1h

l2-l1

∴S扇环=

1

2

l2(a+h)-

1

2

l1a=

1

2

(l2-l1)a+

1

2

l2h
=

1

2

(l2-l1)×

l1h

l2-l1

+

1

2

l2h
=

(l1+l2)h

2

∴S扇环=

(l1+l2)h

2

．

点评：本题主要考查了类比推理的思想和方法，考查运算求解能力，解答此题的关键是根据梯形的面积公式类比出扇环的面积公式．