题目内容
(1)已知k,n∈N*且 k≤n,求证:k
=n
.
(2)已知数列{an}满足an=(n+2)•2n-1-1(n∈N*),是否存在等差数列{bn},使 an=
bk
对一切n∈N*均成立?若存在,求出数列{bn}的通项公式bn;若不存在,说明理由.
| C | k n |
| C | k-1 n-1 |
(2)已知数列{an}满足an=(n+2)•2n-1-1(n∈N*),是否存在等差数列{bn},使 an=
| n |
 |
| k=1 |
| C | k n |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)利用组合数公式,即可证明结论;
(2)利用二项展开式,结合(1)的结论,即可求出数列{bn}的通项公式bn.
(2)利用二项展开式,结合(1)的结论,即可求出数列{bn}的通项公式bn.
解答:
(1)证明:kCnk=k•
=
=n•Cn-1k-1.--(5分)
(2)解:an=(n+2)(1+1)n-1-1=(n+2)(
+
+
+…+
)-1
=n(
+
+
+…+
)+2(
+
+
+…+
)-1
=(n
+n
+n
+…+n
)+2n-1
∵kCnk=nCn-1k-1,
∴(n
+n
+n
+…+n
)=1•Cn1+2•Cn2+3•Cn3+…+n•Cnn.
又2n-1=(1+1)n-1=
+
+
+…+
-1=
+
+…+
故an=(n
+n
+n
+…+n
)+2n-1
=(1•Cn1+2•Cn2+3•Cn3+…+n•Cnn)+(
+
+…+
)
=2•Cn1+3•Cn2+4•Cn3+…+(n+1)•Cnn
即2•Cn1+3•Cn2+4•Cn3+…+(n+1)•Cnn=b1•Cn1+b2•Cn2+…+bn•Cnn,
∴bn=n+1,∴bn-1=n,bn-bn-1=1与n无关.
∴存在等差数列{bn},且通项公式为bn=n+1-----(14分)
| n! |
| k!(n-k)! |
| n•(n-1)! |
| (k-1)![(n-1)-(k-1)]! |
(2)解:an=(n+2)(1+1)n-1-1=(n+2)(
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
=n(
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
=(n
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
∵kCnk=nCn-1k-1,
∴(n
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
又2n-1=(1+1)n-1=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | n n |
故an=(n
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
=(1•Cn1+2•Cn2+3•Cn3+…+n•Cnn)+(
| C | 1 n |
| C | 2 n |
| C | n n |
=2•Cn1+3•Cn2+4•Cn3+…+(n+1)•Cnn
即2•Cn1+3•Cn2+4•Cn3+…+(n+1)•Cnn=b1•Cn1+b2•Cn2+…+bn•Cnn,
∴bn=n+1,∴bn-1=n,bn-bn-1=1与n无关.
∴存在等差数列{bn},且通项公式为bn=n+1-----(14分)
点评:本题考查由数列递推式求数列通项、数列求和;考查推理论证能力、运算求解能力,考查特殊与一般思想.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图是一个几何体的三视图,根据图中数据:
如图是一个几何体的三视图,根据图中数据: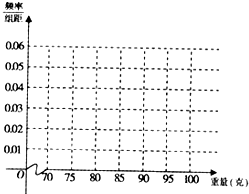 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表: