题目内容
已知函数f(x)=
sin2x+sinxcosx
(Ⅰ)求函数f(x)在区间[
,π]上的零点;
(Ⅱ)设g(x)=f(x)-
,求函数g(x)的图象的对称轴方程和对称中心.
| 3 |
(Ⅰ)求函数f(x)在区间[
| π |
| 2 |
(Ⅱ)设g(x)=f(x)-
| ||
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式和两角和公式化简,令f(x)=0,求得x,则函数在区间上的零点可得.
(Ⅱ)求得g(x)的解析式,利用正弦函数图象与性质求得函数的对称轴方程和对称中心.
(Ⅱ)求得g(x)的解析式,利用正弦函数图象与性质求得函数的对称轴方程和对称中心.
解答:
解:(Ⅰ)f(x)=
-
cos2x+
sin2x=sin(2x-
)+
,
令f(x)=sin(2x-
)+
=0,求得sin(2x-
)=-
,
∴x=kπ或x=kπ-
,k∈Z,
∵x∈[
,π],
∴x=π或
.当x=π时,
∴函数的在区间上的零点为(π,0),(
,0)
(Ⅱ)g(x)=sin(2x-
),
令2x-
=kπ+
,x=
+
,k∈Z,
故函数的对称轴方程为x=
+
,k∈Z,
令2x-
=kπ,x=
+
,k∈Z,
∴函数的对称中心为(
+
,0)(k∈Z).
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
令f(x)=sin(2x-
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∴x=kπ或x=kπ-
| π |
| 6 |
∵x∈[
| π |
| 2 |
∴x=π或
| 5π |
| 6 |
∴函数的在区间上的零点为(π,0),(
| 5π |
| 6 |
(Ⅱ)g(x)=sin(2x-
| π |
| 3 |
令2x-
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
故函数的对称轴方程为x=
| kπ |
| 2 |
| 5π |
| 12 |
令2x-
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
∴函数的对称中心为(
| kπ |
| 2 |
| π |
| 6 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.要求学生对三角函数的对称方程,对称中心,单调性,最值能全面掌握.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
数列{an}前六项是1,2,4,8,16,它的一个通项公式是( )
| A、an=2n |
| B、an=2n |
| C、an=2n+1 |
| D、an=2n-1 |
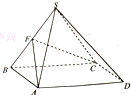 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2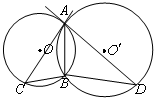 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD. 如图是一个几何体的三视图,根据图中数据:
如图是一个几何体的三视图,根据图中数据: