题目内容
已知数列{an}的前n项和为Sn,首项为a1,且1,an,Sn等差数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列{
}的前n项和,若对于?n∈N*,总有Tn<
成立,求其中m的值.
(1)求数列{an}的通项公式;
(2)设Tn为数列{
| 1 |
| an |
| m-4 |
| 3 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)根据1,an,Sn成等差数列,建立条件关系,利用构造法进行化简,由此能求出an.
(2)判断数列{
}是等比数列,根据数列的前n项和公式,即可解不等式.
(2)判断数列{
| 1 |
| an |
解答:
解:(1)∵1,an,Sn成等差数列,
∴2an=Sn+1,
当n=1时,2a1=a1+1,∴a1=1,
当n≥2时,Sn=2an-1,Sn-1=2an-1-1
两式相减得an=2an-2an-1,
即an=2an-1,
∴数列{an}是以1为首项,2为公比的等比数列,
∴an=a1•2n-1=1•2n-1=2n-1.
(2)∵an=2n-1,∴
=(
)n-1为公比q=
的等比数列,
则Tn=
=2-(
)n-1,
由Tn<
得2-(
)n-1<
,
即m>10-3•(
)n-1,
∵0<(
)n-1≤1,∴-1≤-(
)n-1<0,
∴7≤10-3•(
)n-1<10,
∴m≥10.
∴2an=Sn+1,
当n=1时,2a1=a1+1,∴a1=1,
当n≥2时,Sn=2an-1,Sn-1=2an-1-1
两式相减得an=2an-2an-1,
即an=2an-1,
∴数列{an}是以1为首项,2为公比的等比数列,
∴an=a1•2n-1=1•2n-1=2n-1.
(2)∵an=2n-1,∴
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
则Tn=
1-(
| ||
1-
|
| 1 |
| 2 |
由Tn<
| m-4 |
| 3 |
| 1 |
| 2 |
| m-4 |
| 3 |
即m>10-3•(
| 1 |
| 2 |
∵0<(
| 1 |
| 2 |
| 1 |
| 2 |
∴7≤10-3•(
| 1 |
| 2 |
∴m≥10.
点评:本题主要考查等差数列和等比数列的应用,要求熟练掌握相应的公式,考查学生的计算能力.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
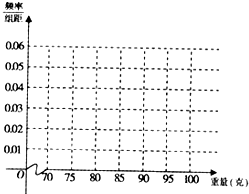 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表: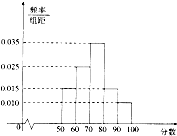 某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为
某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为