题目内容
设集合A是函数f(x)=
+lg(3-x)的定义域,集合B是函g(x)=2x+1的值域.
(Ⅰ)求集A∩B;
(Ⅱ)设集合C={x|x<a},若集合A∩C=A,求实数a的取值范围.
| x+1 |
(Ⅰ)求集A∩B;
(Ⅱ)设集合C={x|x<a},若集合A∩C=A,求实数a的取值范围.
考点:交集及其运算
专题:集合
分析:(Ⅰ)求出f(x)的定义域确定出A,求出g(x)的值域确定出B,找出A∩B即可;
(Ⅱ)由A与C的交集为A,得到A为C的子集,确定出a的范围即可.
(Ⅱ)由A与C的交集为A,得到A为C的子集,确定出a的范围即可.
解答:
解:(Ⅰ)由f(x)=
+lg(3-x),得到
,
解得:-1≤x<3,即A=[-1,3),
由g(x)=2x+1≥1,得到B=[1,+∞),
则A∩B=[1,3);
(Ⅱ)∵C=(-∞,a),且A∩C=A,
∴A⊆C,
则a≥3.
| x+1 |
|
解得:-1≤x<3,即A=[-1,3),
由g(x)=2x+1≥1,得到B=[1,+∞),
则A∩B=[1,3);
(Ⅱ)∵C=(-∞,a),且A∩C=A,
∴A⊆C,
则a≥3.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)的定义域(-1,0),则函f(2x-1)的定义域为( )
| A、(-1,1) | ||
B、(
| ||
| C、(-1,0) | ||
D、(0,
|
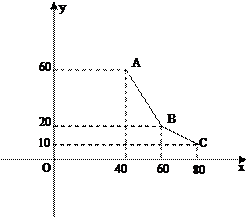 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.