Question

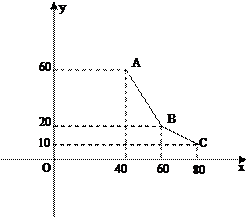小张经营某一消费品专卖店，已知该消费品的进价为每件40元，该店每月销售量y（百件）与销售单价x（元/件）之间的关系用如图的一折线表示，职工每人每月工资为1000元，该店还应交付的其它费用为每月10000元．
（1）把y表示为x的函数；
（2）当销售价为每件50元时，该店正好收支平衡，求该店的职工人数；
（3）若该店只有20名职工，问销售单价定为多少元时，该专卖店月利润最大？（利润=收入-支出）

Answer 1

考点：函数最值的应用

专题：函数的性质及应用

分析：（1）直接分段写出两个一次函数的解析式；
（2）设出该店拥有职工的人数，求出当x=50时该店的总收入，由收支平衡列式得答案；
（3）分段写出该店只有20名职工的月利润：S=

(-2x+140)(x-40)×100-30000，(40≤x≤60) (- 1 2 x+50)(x-40)×100-30000，(60＜x≤80)

，然后分段求出最值得答案．

解答： 解：（1）当40≤x≤60时，由两点式得AB：

y-60

20-60

=

x-40

60-40

，
即y=-20x+140；
当60＜x≤80时，由两点式得BC：

y-20

10-20

=

x-60

80-60

，
即y=-

1

2

x+50；
∴y=

-2x+140，(40≤x≤60) - 1 2 x+50，(60＜x≤80)

；
（2）设该店拥有职工m名，当x=50时，该店的总收入为
y（x-40）×100=100（-2x+140）（x-40）=40000元．
又该店的总支出为1000m+10000元，
依题意得40000=1000m+10000，解得：m=30．
∴此时该店有职工30名；
（3）若该店只有20名职工，则月利润：
S=

(-2x+140)(x-40)×100-30000，(40≤x≤60) (- 1 2 x+50)(x-40)×100-30000，(60＜x≤80)

．
当40≤x≤60时，S=-2（x-55）²+15000，
∴x=55时，S取最大值15000元；
当60＜x≤80时，S=-

1

2

(x-70)2+15000，
∴x=70时，S取最大值15000元；
故当x=55或x=70时，S取最大值15000元，
即销售单价定为55或70元时，该专卖店月利润最大．

点评：本题考查了函数解析式的求解及常用方法，考查了简单的数学建模思想方法，训练了分段函数最值的求法，是中档题．