Question

已知

a

，

b

，

c

，满足|

a

|=1，|

b

|=

2

，

a

，

b

夹角为

π

4

，（

c

-

b

）•（

c

-

a

）=0，则|

c

|的最大值为

 

．

Answer 1

考点：数量积表示两个向量的夹角,向量的模

专题：平面向量及应用

分析：建坐标系系，可得

b

=（1，1），

a

=（1，0），设

c

=（x，y），由垂直关系可得（x-1）²+（y-

1

2

）²=

1

4

，三角换元可得x=1+

1

2

cosθ，y=

1

2

+

1

2

sinθ，由三角函数的知识可得|

c

|=

x2+y2

的最大值，也可用法二几何意义来求．

解答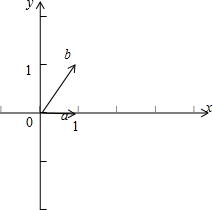： 解：由题意建立如图所示的坐标系，
可得

b

=（1，1），

a

=（1，0），设

c

=（x，y），
∴

c

-

b

=（x-1，y-1），

c

-

a

=（x-1，y），
∵（

c

-

b

）•（

c

-

a

）=0，∴（x-1）²+y（y-1）=0，
配方变形可得（x-1）²+（y-

1

2

）²=

1

4

，
法一：设x-1=

1

2

cosθ，y-

1

2

=

1

2

sinθ，
∴x=1+

1

2

cosθ，y=

1

2

+

1

2

sinθ，
∴x²+y²=（1+

1

2

cosθ）²+（

1

2

+

1

2

sinθ）²=

3

2

+cosθ+

1

2

sinθ，
由三角函数的知识可知cosθ+

1

2

sinθ的最大值为

5

2

，
∴x²+y²=

3

2

+cosθ+

1

2

sinθ的最大值为

3+ 5

2

，
∴|

c

|=

x2+y2

最大值为

5 +1

2

法二：由（x-1）²+（y-

1

2

）²=

1

4

可知点（x，y）
为（1，

1

2

）为圆心

1

2

为半径的圆上的点，
|

c

|=

x2+y2

表示圆上的点到原点的距离，
∴所求最大值为原点到（1，

1

2

）的距离加上圆的半径，
∴所求的最大为

1

2

+

12+( 1 2 )2

=

5 +1

2

故答案为：

5 +1

2

点评：本题考查平面向量的夹角，涉及向量的模长公式以及三角换元的应用，建系是解决问题的关键，属中档题．