题目内容
已知函数f（x）=4x2-kx-8在[4，10]上具有单调性，实数k的取值范围是 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：先求出函数的对称轴，结合二次函数的单调性，从而得到答案．
解答：
解：∵对称轴x=
，
∴只需
≥10或
≤4，
∴k≥80或k≤32，
故答案为：k≥80或k≤32．
| k |
| 8 |
∴只需
| k |
| 8 |
| k |
| 8 |
∴k≥80或k≤32，
故答案为：k≥80或k≤32．
点评：本题考查了函数的单调性，考查了二次函数的性质，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知a是函数f（x）=3x-log
x的零点，若0＜x0＜a，则f（x0）的值满足（ ）
| 1 |
| 3 |
| A、f（x0）＜0 |
| B、f（x0）＞0 |
| C、f（x0）=0 |
| D、f（x0）的符号不确定 |
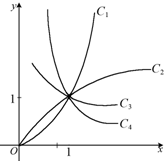如图是幂函数y=xn在第一象限内的图象，已知n取| 1 |
| 2 |
| 1 |
| 2 |
A、2，
| ||||
B、-2，-
| ||||
C、-
| ||||
D、2，
|
已知集合A={x|x＜2
}，a=2，则下列关系正确的是（ ）
| 3 |
| A、a?A | B、{a}∈A |
| C、a∈A | D、a∉A |
若a=0.32，b=20.3，c=log0.32，则a，b，c由大到小的关系是（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、b＞c＞a |
| D、c＞a＞b |
已知函数f（x）=loga
（a＞0，且 a≠1），则（ ）
| 1+x |
| 1-x |
| A、f（x）是R上的奇函数 |
| B、f（x）是R上的偶函数 |
| C、f（x）在定义域上是奇函数 |
| D、以上均不正确 |