题目内容
18. 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.(Ⅰ)求f(x)的最大值及相应的x值;
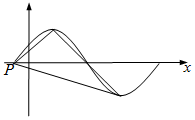
(Ⅱ)设函数$g(x)=f(\frac{π}{4}x)$,如图,点P,M,N分别是函数y=g(x)图象的零值点、最高点和最低点,求cos∠MPN的值.
分析 (Ⅰ)化简函数(x)为正弦型函数,利用正弦函数的图象与性质求出它的最大值以及此时对应的x值;
(Ⅱ)化简函数g(x),过D作MD⊥x轴于D,根据三角函数的对称性求出∠PMN=90°,再求cos∠MPN的值.
解答 解:(Ⅰ)函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$
=sin2x+$\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sin2x…(1分)
=$\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x$
=$sin(2x+\frac{π}{3})$;…(3分)
∴f(x)的最大值为f(x)max=1,…(4分)
此时$2x+\frac{π}{3}=2kπ+\frac{π}{2}$,…(5分)
解得$x=kπ+\frac{π}{12},k∈Z$;…(6分)
(Ⅱ)函数$g(x)=f(\frac{π}{4}x)$=sin[2($\frac{π}{4}$x)+$\frac{π}{3}$]=sin($\frac{π}{2}$x+$\frac{π}{3}$),…(7分)
过D作MD⊥x轴于D,如图所示;
∵PD=DM=1,
∴∠PMN=90°,…(9分)
计算PM=$\sqrt{2}$,MN=2PM=2$\sqrt{2}$,PN=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,…(11分)
∴$cos∠MPN=\frac{{\sqrt{2}}}{{\sqrt{10}}}=\frac{{\sqrt{5}}}{5}$.…(13分)
点评 本题考查了三角函数的化简与运算问题,也考查了三角函数的计算问题,是综合题.

练习册系列答案
相关题目
9.设i是虚数单位,$\overline z$是复数z的共轭复数,若$z=\frac{2}{-1+i}$,则$\overline z$=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
13.设$a={log_2}\frac{1}{5}$,$b={log_3}\frac{1}{5}$,c=2-0.1,则a,b,c间的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
3.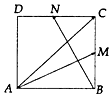 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
7.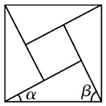 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
 《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )
《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为α、β,且小正方形与大正方形面积之比为4:9,则cos(α-β)的值为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | 0 |
8.若数列{an}的前n项和为Sn,S2n-12+S2n2=4(a2n-2),则2a1+a100=( )
| A. | -8 | B. | -6 | C. | 0 | D. | 2 |