题目内容
13.设$a={log_2}\frac{1}{5}$,$b={log_3}\frac{1}{5}$,c=2-0.1,则a,b,c间的大小关系是( )| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵$a={log_2}\frac{1}{5}$<$b={log_3}\frac{1}{5}$<0,c=2-0.1>0,
∴c>b>a.
故选:A.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.已知f(x)为定义在$(0,\frac{π}{2})$上的函数,f'(x)是它的导函数,且$\frac{f'(x)}{tanx}<f(x)$恒成立,则( )
| A. | $f(\frac{π}{3})<\sqrt{3}f(\frac{π}{6})$ | B. | $f(\frac{π}{6})<\sqrt{2}f(\frac{π}{4})$ | C. | $f(\frac{π}{3})<f(\frac{π}{4})$ | D. | $f(\frac{π}{4})<\sqrt{3}f(\frac{π}{3})$ |
1.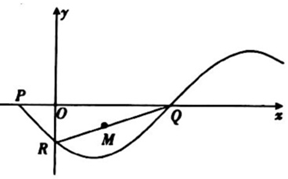 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )| A. | 1 | B. | -1 | C. | $\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{6}}{2}$ |
8.等差数列{an}中,a7=4,a8=1,则a10=( )
| A. | -5 | B. | -2 | C. | 7 | D. | 10 |
5.若对于任意实数m∈[0,1],总存在唯一实数x∈[-1,1],使得m+x2ex-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $({1+\frac{1}{e},e}]$ | C. | (0,e] | D. | $[{1+\frac{1}{e},e}]$ |
3.从含有质地均匀且大小相同的2个红球、n个白球的口袋中随机取出一球,若取到红球的概率是$\frac{2}{5}$,则取得白球的概率等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
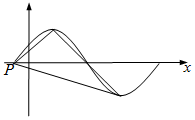 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.