题目内容
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ y≥ax\end{array}\right.$,且目标函数z=3x-2y的最大值为32,负数a=$-\frac{1}{2}$.分析 由题意可得-1<a<0,再由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数即可求得a值.
解答 解:∵a<0,且目标函数z=3x-2y有最大值,∴-1<a<0.
由约束条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ y≥ax\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x+y=4}\\{y=ax}\end{array}\right.$,解得A($\frac{4}{a+1}$,$\frac{4a}{a+1}$).
化目标函数z=3x-2y为y=$\frac{3}{2}x-\frac{z}{2}$,
由图可知,当直线y=$\frac{3}{2}x-\frac{z}{2}$过A时,直线在y轴上的截距最小,z有最大值为$\frac{12}{a+1}-\frac{8a}{a+1}=\frac{12-8a}{a+1}=32$,解得a=$-\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
18.某学校食堂推出两款优惠套餐,甲、乙、丙三位同学选择同一款餐的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
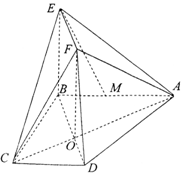 如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.
如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.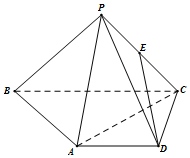 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.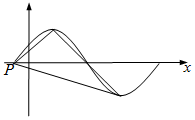 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.