题目内容
10.在空间直角坐标系O-xyz中,一个四面体的四个顶点坐标分别是(0,0,0),(0,3,1),(2,3,0),(2,0,1),则它的外接球的表面积为14π.分析 由题意,四面体的外接球就是长宽高为3,2,1的长方体的外接球,其直径为长方体的对角线$\sqrt{9+4+1}$=$\sqrt{14}$,求出半径,即可求出四面体的外接球的表面积.
解答 解:由题意,四面体的外接球就是长宽高为3,2,1的长方体的外接球,
其直径为长方体的对角线$\sqrt{9+4+1}$=$\sqrt{14}$,半径为$\frac{\sqrt{14}}{2}$,
∴四面体的外接球的表面积为4π•$\frac{14}{4}$=14π.
故答案为14π.
点评 本题考查四面体的外接球的表面积,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
1.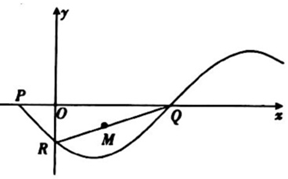 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象与坐标轴的三个交点分别为P(-1,0),Q、R,且线段RQ的中点M的坐标为($\frac{3}{2}$,-$\frac{1}{2}$),则f(-2)等于( )| A. | 1 | B. | -1 | C. | $\frac{\sqrt{6}}{2}$ | D. | -$\frac{\sqrt{6}}{2}$ |
5.若对于任意实数m∈[0,1],总存在唯一实数x∈[-1,1],使得m+x2ex-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $({1+\frac{1}{e},e}]$ | C. | (0,e] | D. | $[{1+\frac{1}{e},e}]$ |
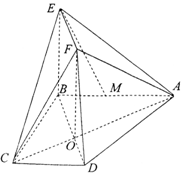 如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.
如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.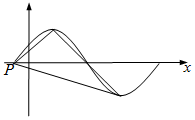 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.