Question

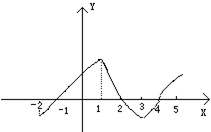如图是y=f（x）的导函数f′（x）的图象，对于下列四个判断：
①f（x）在[-2，-1]上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在[-1，2]上是增函数，在[2，4]上是减函数；
④f（x）有三个极值点．
其中正确的判断是

 

．（填序号）

Answer 1

考点：利用导数研究函数的单调性,利用导数研究函数的极值

专题：导数的综合应用

分析：通过图象，结合导函数的符号，根据函数单调性，极值和导数之间的关系，逐一进行判断，即可得到结论．

解答： 解：由导函数的图象可得：

x	[-2，-1）	-1	（-1，2）	2	（2，4）	4	（4，5）
f′（x）	-	0	+	0	-	0	+
f（x）	单减	极小	单增	极大	单减	极小	单增

①由表格可知：f（x）在区间[-2，-1]上是减函数，因此不正确；
②x=-1是f（x）的极小值点，正确；
③f（x）在[-1，2]上是增函数，在[2，4]上是减函数，正确；
④x=-1，2，4是f（x）的极值点，故f（x）有三个极值点，因此正确．
综上可知：②③④正确．
故答案为：②③④

点评：本小题考查导数的运用以及看图能力．注意看清图画的是导函数的图象，不要与函数图象混淆．