题目内容
定义在R上的偶函数f(x),对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[-1,3]内,函数y=f(x)与函数y=kx+k的图象恰有4个交点,则实数k的取值范围是 .
考点:函数的零点与方程根的关系,抽象函数及其应用
专题:函数的性质及应用
分析:由题意可得,函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,数形结合求得k的范围.
解答:
 解:由题意可得,函数f(x)的周期为2,x∈[-1,1]时,f(x)=x2,
解:由题意可得,函数f(x)的周期为2,x∈[-1,1]时,f(x)=x2,
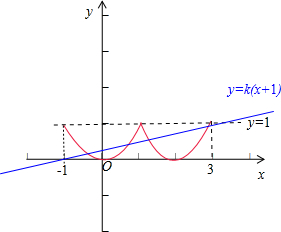
函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,
如图所示:
故有 0<k(3+1)≤1,求得0<k≤
,
故答案为(0,
].
 解:由题意可得,函数f(x)的周期为2,x∈[-1,1]时,f(x)=x2,
解:由题意可得,函数f(x)的周期为2,x∈[-1,1]时,f(x)=x2,函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,
如图所示:
故有 0<k(3+1)≤1,求得0<k≤
| 1 |
| 4 |
故答案为(0,
| 1 |
| 4 |
点评:本题主要考查函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
设离散型随机变量ξ的概率分布如下表:
则P的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| Pi |
|
|
| P |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在三棱锥P-ABC中,除棱PC外,其余棱均等长,M为棱AB的中点,O为线段MC上靠近点M的三等分点.
如图,在三棱锥P-ABC中,除棱PC外,其余棱均等长,M为棱AB的中点,O为线段MC上靠近点M的三等分点.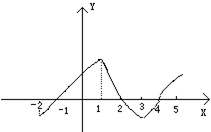 如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断:
如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断: