题目内容
若f(x)=xsinx+cosx,则f(-3),f(
),f(2)的大小关系为 .
| π |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由f(-x)=f(x)知,函数f(x)为偶函数,得f(-3)=f(3).又f′(x)=sin x+xcos x-sin x=xcos x,从而f(x)在区间(
,π)上是减函数,得f(
)>f(2)>f(3)=f(-3).
| π |
| 2 |
| π |
| 2 |
解答:
解:由f(-x)=f(x)知,函数f(x)为偶函数,
因此f(-3)=f(3).
又f′(x)=sinx+xcosx-sinx=xcosx,
当x∈(0,
)时,f′(x)>0,x∈(
,π)时,f′(x)<0,
∴f(x)在区间(
,π)上是减函数,
∴f(
)>f(2)>f(3)=f(-3),
故答案为:f(
)>f(2)>f(-3).
因此f(-3)=f(3).
又f′(x)=sinx+xcosx-sinx=xcosx,
当x∈(0,
| π |
| 2 |
| π |
| 2 |
∴f(x)在区间(
| π |
| 2 |
∴f(
| π |
| 2 |
故答案为:f(
| π |
| 2 |
点评:本题考察了函数的单调性,偶函数的定义,导数的应用,是一道基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
设单位向量
、
的夹角为60°,则向量
+
与向量
的夹角为( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| A、30° | B、60° |
| C、120° | D、150° |
已知x,y满足
且目标函数z=3x+y的最小值是5,则z的最大值是( )
|
| A、8 | B、9 | C、10 | D、12 |
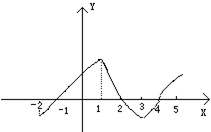 如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断:
如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断: