题目内容
设随机变量X~N(2,4),则D(
X)的值等于( )
| 1 |
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:利用正态分布知识求解.
解答:
解:∵随机变量X~N(2,4),
∴方差DX=4,
∴D(
X)=
DX=1.
故选:A.
∴方差DX=4,
∴D(
| 1 |
| 2 |
| 1 |
| 4 |
故选:A.
点评:本题考查方差的求法,是基础题,解题时要认真审题,注意正态分布知识的合理运用.

练习册系列答案
相关题目
设单位向量
、
的夹角为60°,则向量
+
与向量
的夹角为( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| A、30° | B、60° |
| C、120° | D、150° |
已知f(x)是R上的奇函数,且f(x+4)=f(x),当x∈(-2,0)时,f(x)=2x,则f(2012)-f(2011)( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
设离散型随机变量ξ的概率分布如下表:
则P的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| Pi |
|
|
| P |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知平向向量
,
满足:|
|=1,|
|=6,
•(
-
)=2,则向量
与向量
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x,y满足
且目标函数z=3x+y的最小值是5,则z的最大值是( )
|
| A、8 | B、9 | C、10 | D、12 |
圆台的母线与轴的夹角为30°,母线长为2,一个底面的半径是另一个底面半径的2倍,则两底面面积之和为( )
| A、π | B、3π | C、5π | D、7π |
已知f(x)=
,存在x2>x1≥0使得f(x1)=f(x2),则x1•f(x2)的取值范围( )
|
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
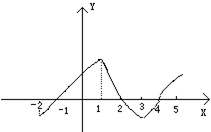 如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断:
如图是y=f(x)的导函数f′(x)的图象,对于下列四个判断: