题目内容

数列{an}的前n项和Sn=2n2-3n+1，则a4+a5+…+a10=
 
．
考点：数列的求和
专题：等差数列与等比数列
分析：a4+a5+…+a10=S10-S3，由此能求出结果．
解答： 解：∵列{an}的前n项和Sn=2n2-3n+1，
∴a4+a5+…+a10=S10-S3
=（2×102-3×10+1）-（2×32-3×3+1）
=161．
故答案为：161．
点评：本题考查数列的前n项和的求法，解题时要认真审题，是基础题．
练习册系列答案
相关题目
如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC=60°，平面AA1C1C⊥平面ABCD，∠A1AC=60°．
（1）证明：BD⊥AA1；
（2）求二面角A1-C1D-B的平面角的余弦值．
已知正三角形的两个顶点是O（0，0）和A（6，0），则它的外接圆的方程是
 
．
根据如图所示的程序框图回答下列问题：如果输入S为20，则输出的i=
 
；如果输出的i为3，则输入的S的取值范围是
 
．
已知集合I={1，2，3，4，5}，选择I的两个非空集合A和B，满足A中最大的数小于B中最小的数，则不同的选择方法总数等于
 
．
如图ABCD是空间四边形，E、F、G、H分别是四边上的点，它们共面，且AC∥平面EFGH，BD∥平面EFGH，AC=m，BD=n，则当四边形EFGH是菱形时，AE：EB=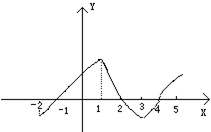
 
．
已知函数g（x）=ln（4x-x2）的定义域为A，B=（-∞，-1]∪[3，+∞），则A∩B=
 
．
如图是y=f（x）的导函数f′（x）的图象，对于下列四个判断：
①f（x）在[-2，-1]上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在[-1，2]上是增函数，在[2，4]上是减函数；
④f（x）有三个极值点．
其中正确的判断是
 
．（填序号）
设单位向量
e1
、
e2
的夹角为60°，则向量
e1
+
e2
与向量
e1
的夹角为（　　）
A、30°B、60°
C、120°D、150°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网