题目内容
若圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
考点:直线与圆相交的性质
专题:直线与圆
分析:直线与圆有两个交点,那么圆心到直线的距离小于半径,得到关于m的不等式解之.
解答:
解:因为圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,圆心为(1,0),半径为1,
所以圆心到直线的距离小于1,即
<1,整理得3m2<1,解得-
<m<
;
故选A.
所以圆心到直线的距离小于1,即
| |-m-m| | ||
|
| ||
| 3 |
| ||
| 3 |
故选A.
点评:本题考查了直线与圆的位置关系;如果直线与圆相交,那么圆心到直线的距离小于半径.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列四个命题正确的是( )
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
④随机误差e是衡量预报精确度的一个量,它的平均值为0.
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
④随机误差e是衡量预报精确度的一个量,它的平均值为0.
| A、①③ | B、②④ | C、①④ | D、②③ |
函数f(x)=
的零点个数为( )
|
| A、3 | B、2 | C、1 | D、0 |
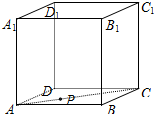 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题: