题目内容
已知函数f(x)=x-2m2+m+3(m∈Z)是增函数,也是偶函数
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga[f(x)-ax](a>0且a≠1),是否存在实数a,使g(x)在区间[2,3]上的最大值为2,若存在,请求出a的值,若不存在,请说明理由.
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga[f(x)-ax](a>0且a≠1),是否存在实数a,使g(x)在区间[2,3]上的最大值为2,若存在,请求出a的值,若不存在,请说明理由.
考点:幂函数的性质
专题:函数的性质及应用
分析:本题(1)根据指数函数为增函数,得到指数的取值范围,再利用函数为偶函数和整数条件,得到m的值,从而求出f(x)的解析式,得到本题结论;(2)可以先将g(x)在区间[2,3]上的最大值问题转化为内函数h(x)=x2-ax在区间上的最值问题,通过分类讨论,研究二次函数在区间上的值域,得到本题结论.
解答:
解:(1)由条件知幂函数f(x)=x-2m2+m+3(m∈Z)在(0,+∞)上为增函数,
∴-2m2+m+3>0,
∴-1<m<
,
又m∈Z,
∴m=0或1.
当m=0时,f(x)=x3,不满足f(x)为偶函数;
当m=1时,f(x)=x2,满足f(x)为偶函数;
∴f(x)=x2.
(2)g(x)=loga(x2-ax),
令h(x)=x2-ax,
由h(x)>0得:x∈(-∞,0)∪(a,+∞),
∵g(x)在[2,3]上有定义,
∴0<a<2且a≠1,
∴h(x)=x2-ax在[2,3]上为增函数.
1°当1<a<2时,gmax=g(3)=loga(9-3a)=2,
∴a2+3a-9=0⇒a=
∵1<a<2,∴a=
;
2°当0<a<1时,gmax=g(2)=loga(4-2a)=2,
∴a2+2a-4=0⇒a=-1±
,
∵0<a<1,
∴此种情况不存在,
综上,存在实数a=
,使g(x)在区间[2,3]上的最大值为2.
∴-2m2+m+3>0,
∴-1<m<
| 3 |
| 2 |
又m∈Z,
∴m=0或1.
当m=0时,f(x)=x3,不满足f(x)为偶函数;
当m=1时,f(x)=x2,满足f(x)为偶函数;
∴f(x)=x2.
(2)g(x)=loga(x2-ax),
令h(x)=x2-ax,
由h(x)>0得:x∈(-∞,0)∪(a,+∞),
∵g(x)在[2,3]上有定义,
∴0<a<2且a≠1,
∴h(x)=x2-ax在[2,3]上为增函数.
1°当1<a<2时,gmax=g(3)=loga(9-3a)=2,
∴a2+3a-9=0⇒a=
-3±3
| ||
| 2 |
-3+3
| ||
| 2 |
2°当0<a<1时,gmax=g(2)=loga(4-2a)=2,
∴a2+2a-4=0⇒a=-1±
| 5 |
∵0<a<1,
∴此种情况不存在,
综上,存在实数a=
-3+3
| ||
| 2 |
点评:本题考查了函数的单调性、奇偶性、值域,还考查了分类讨论的数学思想,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
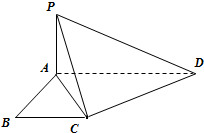 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.