题目内容
数列{an}满足:a1=1,a2=2,an=
(n≥3且n∈N),则a2014=( )
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2-2014 |
考点:数列递推式
专题:等差数列与等比数列
分析:首先根据递推关系式,求出一部分的值,在观察出数列的各项具备的规律,利用周期最后求出结果.
解答:
解:数列{an}满足:a1=1,a2=2,
利用an=
(n≥3且n∈N),
则:a3=
=2 a4=
=1 a5=
=
a6=
=
a7=
=1 a8=
=2
1,2,2,1,
,
,1,2,2,1,
,
,1,2,…
所以:数列的周期为:6
2014=335×6+4
所以:a2014=a4=1
故选:A
利用an=
| an-1 |
| an-2 |
则:a3=
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
| 1 |
| 2 |
| a5 |
| a4 |
| 1 |
| 2 |
| a6 |
| a5 |
| a7 |
| a6 |
1,2,2,1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以:数列的周期为:6
2014=335×6+4
所以:a2014=a4=1
故选:A
点评:本题考查的知识要点:数列递推关系式的应用,数列的周期性在运算中的应用.属于基础题型.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
函数y=sin(
x-
)的最小正周期是( )
| 1 |
| 2 |
| π |
| 10 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
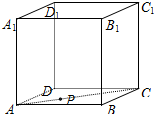 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题: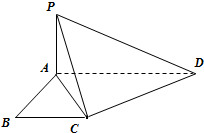 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.