题目内容
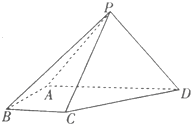 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2| 2 |
(1)求直线PC与平面PAD所成的角;
(2)求二面角A-PB-C的大小.
考点:与二面角有关的立体几何综合题,直线与平面所成的角
专题:空间角
分析:(1)取E为AD的中点,CE⊥平面PAD,∠CPE即PC与平面ABD所成的角;
(2)利用二面角的平面角的定义,作棱的垂线,从而∠AFC即二面角A-PB-C的平面角.
(2)利用二面角的平面角的定义,作棱的垂线,从而∠AFC即二面角A-PB-C的平面角.
解答:
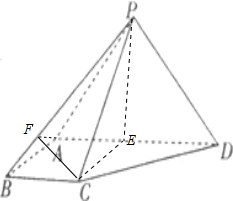 解:(1)取E为AD的中点,连接CE、PE,∵BC∥AD,AB⊥AD,AD=2AB=2BC=2
解:(1)取E为AD的中点,连接CE、PE,∵BC∥AD,AB⊥AD,AD=2AB=2BC=2
,∴正方形ABCE,CE⊥AD,又∵侧面PAD⊥底面ABCD,∴CE⊥平面PAD,∠CPE即PC与平面ABD所成的角,PE=CE=
,∴∠CPE=45°,PC与平面ABD所成的角大小为45°-----------------(6分)
(2)在Rt△PCE中,CE=PE=
,PE=2,PA=PE,AB=AC,PB=PB∴△PAB≌△PCB,在△PAB中作AF⊥PB,垂直F,连CF,则CF⊥PB,∠AFC即二面角A-PB-C的平面角,在△AFC,AF=CF=
,AC=2,cos∠AFC=-
,∴二面角A-PB-C的大小为120°--------------------------(12分)
 解:(1)取E为AD的中点,连接CE、PE,∵BC∥AD,AB⊥AD,AD=2AB=2BC=2
解:(1)取E为AD的中点,连接CE、PE,∵BC∥AD,AB⊥AD,AD=2AB=2BC=2| 2 |
| 2 |
(2)在Rt△PCE中,CE=PE=
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
点评:本题考查线面角、二面角的平面角的计算,应掌握线面角、二面角的平面角的作法是关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
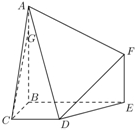 如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.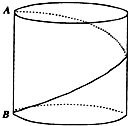 如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
如图,底面半径为1,高为2的圆柱,有A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少? 如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE,求证:
如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE,求证: