题目内容
定义域为R的函数y=f(x),当x>0,f(x)>1,对任意a,b∈R有f(a+b)=f(a)•f(b)
(1)求f(0);
(2)证明对x∈R,有f(x)>0;
(3)证明f(x)在R上为增函数;
(4)若f(x)•f(2x-x2)>1,求x的取值范围.
(1)求f(0);
(2)证明对x∈R,有f(x)>0;
(3)证明f(x)在R上为增函数;
(4)若f(x)•f(2x-x2)>1,求x的取值范围.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)为使f(a+b)=f(a)•f(b)中有f(0),由当x>0时,f(x)>1.可设x=0,y=1可得f(1)=f(0)•f(1),结合f(1)>1可求f(0)
(2)(3)要证明f(x)在R上是增函数,即证明当x1<x2时,有f(x1)<f(x2),当x1,x2∈R,x1<x2,有x2-x1>0,则f(x2)=f(x1+x2-x1)=f(x1)•f(x2-x1),可证
(4)由f(x)•f(2x-x2)>1得到3x-x2>0,解得即可.
(2)(3)要证明f(x)在R上是增函数,即证明当x1<x2时,有f(x1)<f(x2),当x1,x2∈R,x1<x2,有x2-x1>0,则f(x2)=f(x1+x2-x1)=f(x1)•f(x2-x1),可证
(4)由f(x)•f(2x-x2)>1得到3x-x2>0,解得即可.
解答:
(1)解:设a=0,b=1得:f(0+1)=f(0)•f(1),
即f(1)=f(0)•f(1)
∵f(1)>1
∴f(0)=1
(2)证明:∵对x1,x2∈R,x1<x2,有x2-x1>0
∴f(x2)=f(x1+x2-x1)=f(x1)•f(x2-x1)中有f(x2-x1)>1
由已知可,得当x1>0时,f(x1)>1>0
当x1=0时,f(x1)=1>0
当x1<0时,f(x1)•f(-x1)=f(x1-x1)=f(0)=1
又∵f(-x1)>1
∴0<f(x1)<1
故对于一切x1∈R,有f(x1)>0
(3)证明由(2)可知,
∴f(x2)=f(x1)•f(x2-x1)>f(x1),
故f(x)在R上为增函数;
(4)∵f(x)•f(2x-x2)>1,
∴f(x)•f(2x-x2)=f(3x-x2)>1,
∴3x-x2>0,
解得0<x<3
即f(1)=f(0)•f(1)
∵f(1)>1
∴f(0)=1
(2)证明:∵对x1,x2∈R,x1<x2,有x2-x1>0
∴f(x2)=f(x1+x2-x1)=f(x1)•f(x2-x1)中有f(x2-x1)>1
由已知可,得当x1>0时,f(x1)>1>0
当x1=0时,f(x1)=1>0
当x1<0时,f(x1)•f(-x1)=f(x1-x1)=f(0)=1
又∵f(-x1)>1
∴0<f(x1)<1
故对于一切x1∈R,有f(x1)>0
(3)证明由(2)可知,
∴f(x2)=f(x1)•f(x2-x1)>f(x1),
故f(x)在R上为增函数;
(4)∵f(x)•f(2x-x2)>1,
∴f(x)•f(2x-x2)=f(3x-x2)>1,
∴3x-x2>0,
解得0<x<3
点评:本题主要考查了利用抽象函数的赋值法求解函数值,及利用构造法证明函数的单调性的技巧要求考生熟练应用,属于中档题.

练习册系列答案
相关题目
设{an}是等比数列,若a2=3,a7=1,则数列{an}前8项的积为( )
| A、56 | B、80 | C、81 | D、128 |
经过点(-1,0),且与直线x+2y-3=0垂直的直线方程是( )
| A、2x-y+2=0 |
| B、2x+y+2=0 |
| C、2x-y-2=0 |
| D、x-2y+1=0 |
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-2x-2与g(x)=-x+n在[-1,3]上是“关联函数”,则n的取值范围是( )
| A、(-∞,0] | ||
| B、(-∞,4] | ||
C、(-
| ||
D、(-
|
已知{an}为等比数列,a5+a8=2,a6•a7=-8,则a2+a11=( )
| A、5 | B、7 | C、-7 | D、-5 |
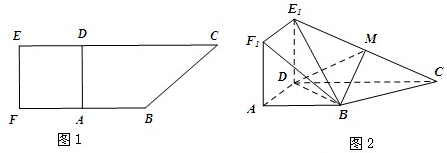
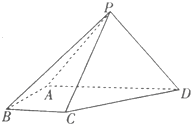 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2