题目内容
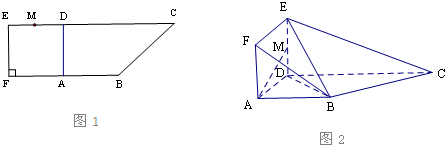
如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=
CD=1.现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.
(1)求证:AM∥平面BEC;
(2)求证:BC⊥平面BDE;
| 1 |
| 2 |
(1)求证:AM∥平面BEC;
(2)求证:BC⊥平面BDE;

考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取EC中点N,连接MN,BN,证明BN∥AM.说明BN?平面BEC,且AM?平面BEC,即可证明AM∥平面BEC;
(2)先证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE.
(2)先证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE.
解答:
证明:(1)取EC中点N,M是EC的中点,连接MN,BN.
在△EDC中,M,N分别为ED,EC的中点,
所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,
所以MN∥AB,且MN=AB.
所以四边形ABNM为平行四边形.
所以BN∥AM.
又因为BN?平面BEC,且AM?平面BEC,
所以AM∥平面BEC.
(2)在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,得BC=
.
在△BCD中,BD=BC=
,
所以BD2+BC2=CD2.
所以BC⊥BD.
所以BC⊥平面BDE.
在△EDC中,M,N分别为ED,EC的中点,
所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |

所以MN∥AB,且MN=AB.
所以四边形ABNM为平行四边形.
所以BN∥AM.
又因为BN?平面BEC,且AM?平面BEC,
所以AM∥平面BEC.
(2)在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
所以BD2+BC2=CD2.
所以BC⊥BD.
所以BC⊥平面BDE.
点评:本题是中档题,考查直线与平面的平行与垂直的证明方法,几何体的体积的解法,考查空间想象能力、计算能力,注意转化思想的应用,判定定理的正确应用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
定义在R上的函数f(x)在(-∞,-2)上是减函数,且f(x-2)的图象关于y轴对称,则( )
| A、f(-3)<f(1) |
| B、f(-3)=f(0) |
| C、f(-3)=f(1) |
| D、f(-3)>f(0) |
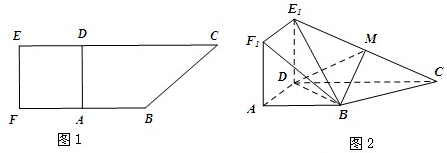
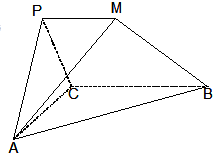 在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2
在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=2PM=4,AB=2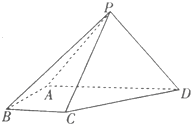 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2