题目内容

已知四边形ABCD是边长为a的正方形，若
DE
=2
EC
，
CF
=2
FB
，则
AE
•
AF
的值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由平面向量基本定理，用
AB
和
AD
作基底表示向量
AE
和
AF
，由平面向量数量积的运算可得答案．
解答： 解：∵
DE
=2
EC
，∴
DE
=
2
3
DC
=
2
3
AB
，
又∵
CF
=2
FB
，∴
BF
=
1
3
BC
=
1
3
AD
，
∴
AE
=
AD
+
DE
=
2
3
AB
+
AD
，
∴
AF
=
AB
+
BF
=
AB
+
1
3
AD
，
∴
AE
•
AF
=（
2
3
AB
+
AD
）•（
AB
+
1
3
AD
）
=
2
3
AB
2+
1
3
AD
2+
11
9
AB
•
AD

=
2
3
a2+
1
3
a2+0=a2
故答案为：a2．
点评：本题考查平面向量数量积的运算，用向量
AB
和
AD
作基底来表示题中的向量是解决问题的关键，属中档题．
练习册系列答案
相关题目
在△ABC中，角A、B、C的对边分别为a、b、c且
b
a
=
sin2C
sinA
．
（Ⅰ）若C=
5
12
π，求角B的大小；
（Ⅱ）若b=2，B≤
π
3
≤C，求△ABC面积的最小值．
设f（x）为定义在R上的奇函数，当x≤0时，f（x）=2x-3x+2m（m为实常数），则f（1）=
 
．
已知关于x，y的二元一次不式组
x+2y≤4
x-y≤1
x+2≥0
，则3x-y的最大值为
 
．
∫
π
2
0
cosxdx=
 
．
（理）在下列命题中：
①若向量
a
、
b
共线，则
a
、
b
所在的直线平行；
②若
a
、
b
所在的直线是异面直线，则向量
a
、
b
一定不共面；
③若
a
、
b
、
c
三向量两两共面，则
a
、
b
、
c
三向量一定也共面；
④已知三向量
a
、
b
、
c
，则空间任意一个向量
p
总可以唯一表示为
p
=x
a
+y
b
+z
c
．
其中正确命题的个数为
 
．
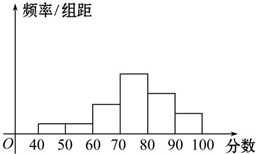从某校参加数学竞赛的试卷中抽取一个样本，考查竞赛的成绩分布，将样本分成6组，得到频率分布直方图如图，从左到右各小组的小长方形的高的比为1：1：3：6：4：2，最右边的一组的频数是8．估计这次数学竞赛成绩的平均数
 
．
下列说法正确的是
 
（请把你认为正确说法的序号都填上）．
①与
a
=（-3，4）共线的单位向量是（-
4
5
，
3
5
）；
②函数f（x）=cos2x+2sin2x的最小正周期为π；
③y=
1-x2
x+|3-x|
是偶函数；
④P是△ABC所在平面内一点，若
PA
•
PB
=
PB
•
PC
=
PC
•
PA
，则P是△ABC的垂心；
⑤若函数y=log
1
2
（x2-2ax+3）的值域为R，则a的取值范围是（-
3
，
3
）．
∫
0
-2
4-x2
dx的值是（　　）
A、4π
B、2π
C、π
D、
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网