题目内容
在△ABC中,角A、B、C的对边分别为a、b、c且
=
.
(Ⅰ)若C=
π,求角B的大小;
(Ⅱ)若b=2,B≤
≤C,求△ABC面积的最小值.
| b |
| a |
| sin2C |
| sinA |
(Ⅰ)若C=
| 5 |
| 12 |
(Ⅱ)若b=2,B≤
| π |
| 3 |
考点:正弦定理的应用
专题:计算题,解三角形
分析:(Ⅰ)由
=
,根据正弦定理,可求角B的大小;
(Ⅱ)先确定A=C,再利用S△ABC=
bhb=tanC≥
,即可求△ABC面积的最小值.
| b |
| a |
| sin2C |
| sinA |
(Ⅱ)先确定A=C,再利用S△ABC=
| 1 |
| 2 |
| 3 |
解答:
(Ⅰ)解:由正弦定理,得
=
=
.
∴sinB=sin2C=sin
π=
.∴B=
(B=
舍).
(Ⅱ)由(Ⅰ)中sinB=sin2C得B=2C或B+2C=π.
又B≤
≤C,∴B+2C=π,∴A=C.
∴S△ABC=
bhb=tanC≥
.
∴当C=
时,S△ABC取最小值
.
| b |
| a |
| sinB |
| sinA |
| sin2C |
| sinA |
∴sinB=sin2C=sin
| 5 |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
(Ⅱ)由(Ⅰ)中sinB=sin2C得B=2C或B+2C=π.
又B≤
| π |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
∴当C=
| π |
| 3 |
| 3 |
点评:本题考查正弦定理,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)>0的解集为( )
| A、{x|x<-2或x>0} |
| B、{x|x<0或x>2} |
| C、{x|x>0} |
| D、{x|x<0} |

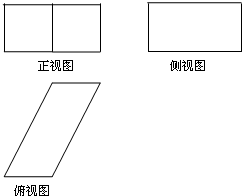 一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为
一个几何体的三视图如图所示.已知正视图为两个边长为1的正方形拼成的矩形,侧视图是一个长为