题目内容
已知函数f(x)=2sin(x-
).
(1)在如下直角坐标系中,用“五点法”画出函数y=f(x)在区间[0,2π]上的简图;
(2)求函数y=f(x)的单调递增区间和递减区间.
| π |
| 4 |
(1)在如下直角坐标系中,用“五点法”画出函数y=f(x)在区间[0,2π]上的简图;
(2)求函数y=f(x)的单调递增区间和递减区间.
考点:五点法作函数y=Asin(ωx+φ)的图象,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)列表描点连线直接用“五点法”画出函数y=f(x)在区间[0,2π]上的简图;
(2)由2kπ-
≤x-
≤2kπ+
,由k∈z,求得x的范围,即得函数的增区间;同理2kπ-
≤x≤2kπ+
,(k∈Z),由即得函数的减区间.
(2)由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
解答:
解:(1)列表:
得到函数的图象如图所示
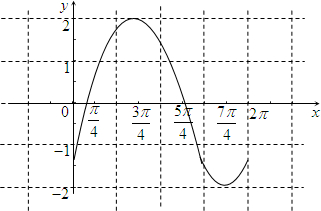
(2)由2kπ-
≤x-
≤2kπ+
得2kπ-
≤x≤2kπ+
,(k∈Z),
即函数y=f(x)的单调递增区间为[2kπ-
,2kπ+
](k∈Z),
同理得单调递减区间为[2kπ+
,2kπ+
](k∈Z)
| x | 0 |
|
|
|
| 2π | ||||||||||
x-
| -
| 0 |
| π |
|
| ||||||||||
| f(x) | -
| 0 | 2 | 0 | -2 | -
|
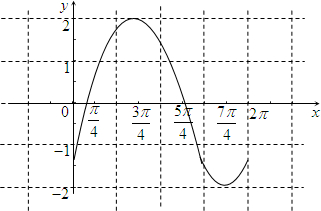
(2)由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
得2kπ-
| π |
| 4 |
| 3π |
| 4 |
即函数y=f(x)的单调递增区间为[2kπ-
| π |
| 4 |
| 3π |
| 4 |
同理得单调递减区间为[2kπ+
| 3π |
| 4 |
| 7π |
| 4 |
点评:本题考查三角函数的单调性,五点作图法,考查了计算能力,作图能力.是中档题.

练习册系列答案
相关题目
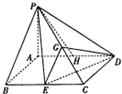 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=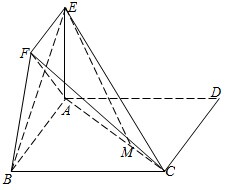 如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,
如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,