题目内容
若函数f(x)的定义域是[-1,5],求函数F(x)=[f(x)]2+f(-x)的定义域.
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:由函数f(x)的定义域是[-1,5]可得x∈[-1,5],-x∈[-1,5],解出即可.
解答:
解:∵函数f(x)的定义域是[-1,5],
∴x∈[-1,5],-x∈[-1,5],
∴x∈[-1,1].
故函数F(x)=[f(x)]2+f(-x)的定义域为[-1,1].
∴x∈[-1,5],-x∈[-1,5],
∴x∈[-1,1].
故函数F(x)=[f(x)]2+f(-x)的定义域为[-1,1].
点评:本题考查了函数的定义域的求法,属于基础题.

练习册系列答案
相关题目
用数学归纳法证明1+
+
+…+
<n(n∈N*,n>1)时,第一步应验证不等式( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
A、1+
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、1+
|
若a>0,b>0,且a+b=4,则ab的最大值为( )
| A、8 | B、4 | C、2 | D、1 |
在△ABC中边a=5,b=6,c=7,则△ABC面积是( )
| A、6 | ||
B、12
| ||
| C、12 | ||
D、6
|
圆x2+y2-4y-1=0的圆心和半径是( )
| A、C(2,0),r=5 | ||
B、C(0,2),r=
| ||
C、C(0,-2),r=
| ||
| D、C(-2,0),r=5 |
设等差数列{an}的前n项和为Sn,若S10-S1=1,则S11等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
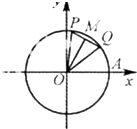 如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为
如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为