Question

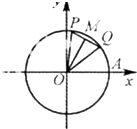如图，P，Q是以原点为圆心的单位圆上的两个动点，若它们同时从点A（1，0）出发，沿逆时针方向作匀角速度运动，其角速度分别为

π

3

，

π

6

（单位：弧度/秒），M为线段PQ的中点，记经过x秒后（其中0≤x≤6），f（x）=|OM|．
（Ⅰ）求y=f（x）的函数解析式；
（Ⅱ）将f（x）图象上的各点均向右平移2个单位长度，得到g=g（x）的图象，求函数g=g（x）的单调递减区间．

Answer 1

考点：余弦函数的单调性,任意角的三角函数的定义

专题：三角函数的图像与性质

分析：（Ⅰ）依题意可知∠POA=

π

3

x，∠QOA=

π

6

x，∠MOQ=

π 3 x- π 6 x

2

=

π

12

x，从而求得f（x）=|OM|=cos∠MOQ 的解析式．
（Ⅱ）依题意可知g（x）=cos（

π

12

x-

π

6

）（2≤x≤8），由2kπ≤

π

12

x-

π

6

≤2kπ+π，求得x的范围，可得函数g=g（x）在[2，8]上的单调递减区间．

解答： 解：（Ⅰ）依题意可知∠POA=

π

3

x，∠QOA=

π

6

x．
∵|OP|=|OQ|=1，∴|OM|=|OQ|•cos∠MOQ=cos∠MOQ，
∴∠MOQ=

π 3 x- π 6 x

2

=

π

12

x，∴f（x）=|OM|=cos

π

12

x（0≤x≤6），
即 f（x）=cos

π

12

x，（0≤x≤6）．
（Ⅱ）依题意可知g（x）=cos

π

12

（x-2）=cos（

π

12

x-

π

6

）（2≤x≤8），
由2kπ≤

π

12

x-

π

6

≤2kπ+π，得 24k+2≤x≤24k+14，
故函数g=g（x）在[2，8]上的单调递减区间为[2，8]．

点评：本题主要考查直角三角形中的边角关系，余弦函数的单调性，属于基础题．