题目内容
15. 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:| 降尘率(%)分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35] |
| 频数 | 10 | 15 | 10 | 25 | 20 | 15 | 5 |
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
分析 (1)绘制频率分步直方图即可,
(2)利用平均值的意义即可得出;
(3)利用频率来估计概率即可.
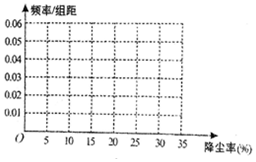
解答  解:(1)其频率依次为0.10,0.15,0.10,0.25,0.20,0.15,0.05,其对应的小长方形的高分别为为0.02,0.03,0.02,0.04,0.05,0.03,0.01,
解:(1)其频率依次为0.10,0.15,0.10,0.25,0.20,0.15,0.05,其对应的小长方形的高分别为为0.02,0.03,0.02,0.04,0.05,0.03,0.01,
则频率分布直方图如图所示:
(2)雾炮降尘率的平均数:2.5×0.1+7.5×0.15+12.5×0.1+17.5×0.25+22.5×0.2+27.5×0.15+32.5×0.05=17.25,
(3)因为第4组为[15,20),且频数为25,故大于等于18小于20的频率大约为$\frac{2}{5}$×0.25=0.10,
故降尘率达到18%以上的频率为0.10+0.20+0.15+0.05=0.5,
故可以用频率来估计概率,雾炮除尘有效的概率:0.5
点评 本题考查了频率分布直方图,熟练掌握平均值的意义、用频率来估计概率,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设复数z=$\frac{1+i}{1-i}$,则z$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | 1 | D. | 2 |
10.已知点A、B在半径为$\sqrt{3}$的球O表面上运动,且AB=2,过AB作相互垂直的平面α、β,若平面α、β截球O所得的截面分别为圆M、N,则( )
| A. | MN长度的最小值是2 | B. | MN的长度是定值$\sqrt{2}$ | ||
| C. | 圆M面积的最小值是2π | D. | 圆M、N的面积和是定值8π |
20.已知复数z=$\frac{2-i}{1+i}$(其中i为虚数单位),则|z|=( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\sqrt{10}$ |