题目内容
10.已知点A、B在半径为$\sqrt{3}$的球O表面上运动,且AB=2,过AB作相互垂直的平面α、β,若平面α、β截球O所得的截面分别为圆M、N,则( )| A. | MN长度的最小值是2 | B. | MN的长度是定值$\sqrt{2}$ | ||
| C. | 圆M面积的最小值是2π | D. | 圆M、N的面积和是定值8π |
分析 作出图象,求出CD,即可得出结论.
解答  解:如图所示,过AB作相互垂直的平面α、β,则BD⊥BC,
解:如图所示,过AB作相互垂直的平面α、β,则BD⊥BC,
BC2+BD2+4=12,∴CD=2$\sqrt{2}$,
∵M,N分别是AC,AD的中点,
∴MN的长度是定值$\sqrt{2}$,
故选B.
点评 本题考查球的内接几何体,考查面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{a}$|=2$\sqrt{3}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$,$\overrightarrow{a}$⊥(3$\overrightarrow{a}$-$\overrightarrow{b}$),则|$\overrightarrow{b}$|等于( )
| A. | 6 | B. | 6$\sqrt{3}$ | C. | 12 | D. | 12$\sqrt{3}$ |
5.已知方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{m+1}$=1表示椭圆,则实数m的取值范围是( )
| A. | (-∞,-1) | B. | (-2,+∞) | C. | (-∞,-$\frac{3}{2}$)∪(-1,+∞) | D. | (-2,-$\frac{3}{2}$)∪(-$\frac{3}{2}$,-1) |
15.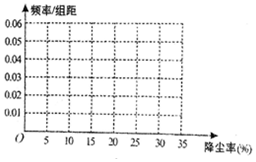 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:| 降尘率(%)分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35] |
| 频数 | 10 | 15 | 10 | 25 | 20 | 15 | 5 |
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
2.已知双曲线M的实轴长为2,且它的一条渐近线方程为y=2x,则双曲线M的标准方程可能是( )
| A. | x2-4y2=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-4x2=1 |
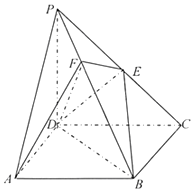 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.