题目内容
7.不超过实数x的最大整数称为x的整数部分,记作[x],已知f(x)=cos([x]-x),给出下列结论:①f(x)是偶函数;
②f(x)是周期函数,且最小正周期为π;
③f(x)的单调递减区间为[k,k+1)(k∈Z);
④f(x)的值域为[cos1,1].
其中正确的结论是( )
| A. | ③ | B. | ①③ | C. | ③④ | D. | ②③ |
分析 作函数f(x)=cos([x]-x)的图象,结合图象逐一核对四个命题得答案.
解答 解:作函数f(x)=cos(x-[x])的图象如下,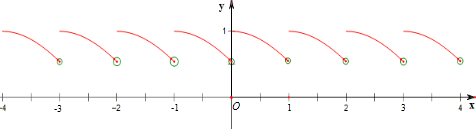
①y=f(x)不是偶函数,故①不正确;
②y=f(x)为周期函数,周期为1,故②不正确;
③当x∈[k,k+1)时,f(x)是单调递减函数,故③正确;
④y=f(x)的最小值不存在,最大值为1,故④不正确;
∴正确结论的序号是③,
故选:A.
点评 本题考查命题的真假判断与应用,考查函数的图象,是中档题.

练习册系列答案
相关题目
17.若全集U={1,2,3,4,5,6,7},集合A={1,3,5,7},集合B={1,4,7},则集合(∁UA)∩B=( )
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
15. 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:| 降尘率(%)分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35] |
| 频数 | 10 | 15 | 10 | 25 | 20 | 15 | 5 |
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
2.已知双曲线M的实轴长为2,且它的一条渐近线方程为y=2x,则双曲线M的标准方程可能是( )
| A. | x2-4y2=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-4x2=1 |
16.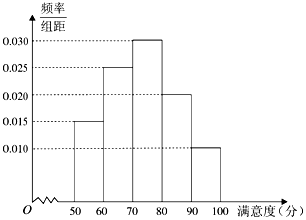 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
(Ⅰ)根据A公司的频率分布直方图,估计该公司满意度评分的中位数;
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:| 满意度 评分分组 | 频数 |
| [50,60) | 2 |
| [60,70) | 8 |
| [70,80) | 14 |
| [80,90) | 14 |
| [90,100] | 2 |
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
8.已知集合A={-$\frac{1}{3}$,$\frac{1}{2}$},B={x|ax+1=0}},且B⊆A,则a的可取值组成的集合为( )
| A. | {-3,2} | B. | {-3,0,2} | C. | {3,-2} | D. | {3,0,-2} |
 团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.