题目内容
5.已知函数f(x)满足f(x+3)=3f(x),当x∈(0,3)时$f(x)=lnx-ax({a>\frac{1}{3}})$,当x∈(-6,-3)时f(x)的最大值为$-\frac{1}{9}$,则实数a的值等于( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 利用条件得出 x∈(-6,-3)时f(x)的最大值为$-\frac{1}{9}$,则y=ln(x+6)-a(x+6)的最大值为-1,即可得出结论.
解答 解:当x∈(-6,-3)时,x+6∈(0,3),
f(x+6)=3f(x+3)=9f(x)=ln(x+6)-a(x+6),
x∈(-6,-3)时f(x)的最大值为$-\frac{1}{9}$,则y=ln(x+6)-a(x+6)的最大值为-1,
y′=$\frac{1}{x+6}$-a,∴x=$\frac{1}{a}$-6时,函数取得最大值-1,
∴ln$\frac{1}{a}$-1=-1,∴a=1,
故选:D.
点评 本题考查导数知识的运用,考查函数的最大值,考查函数解析式的确定,属于中档题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.已知直线l过双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点且与Γ的一条渐近线平行,若l在y轴上的截距为$\sqrt{6}$a,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
13.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )


| A. | $2+\sqrt{5}$ | B. | $2+2\sqrt{5}$ | C. | $4+\sqrt{5}$ | D. | 5 |
10. 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x、y的值,并完成频率分布直方图;
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | [0,50) | [50,100) | [100,150) | [150,200) | [201,250] |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
17.若全集U={1,2,3,4,5,6,7},集合A={1,3,5,7},集合B={1,4,7},则集合(∁UA)∩B=( )
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
15.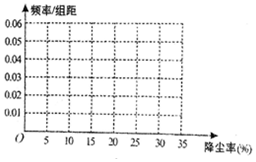 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:| 降尘率(%)分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35] |
| 频数 | 10 | 15 | 10 | 25 | 20 | 15 | 5 |
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
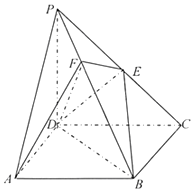 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.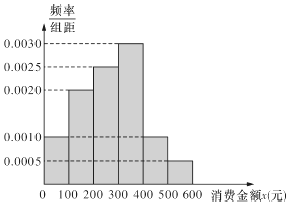 长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).
长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).