题目内容
6.设△ABC的内角A,B,C的对边分别为a,b,c,若c=2$\sqrt{3}$,sinB=2sinA.(1)若C=$\frac{π}{3}$,求a,b的值;
(2)若cosC=$\frac{1}{4}$,求△ABC的面积.
分析 (1)由已知及正弦定理可得b=2a,利用余弦定理可求a的值,进而可求b;
(2)由已知利用同角三角函数基本关系式可求sinC,又b=2a,利用余弦定理可解得c=2a,从而可求a,b,利用三角形面积公式即可计算得解.
解答 (本题满分为12分)
解:(1)∵C=$\frac{π}{3}$,sinB=2sinA,
∴由正弦定理可得:b=2a,…2分
∵c=2$\sqrt{3}$,
∴由余弦定理可得:c2=a2+b2-2abcosC,即:12=a2+4a2-2a2,
∴解得:a=2,b=4…6分
(2)∵cosC=$\frac{1}{4}$,
∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{15}}{4}$,
又∵b=2a,
∴由余弦定理可得:c2=a2+b2-2abcosC=a2+4a2-a2=4a2,解得:c=2a,…9分
∵c=2$\sqrt{3}$,可得:a=$\sqrt{3}$,b=2$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×\sqrt{3}×2\sqrt{3}×\frac{\sqrt{15}}{4}$=$\frac{3\sqrt{15}}{4}$…12分
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若全集U={1,2,3,4,5,6,7},集合A={1,3,5,7},集合B={1,4,7},则集合(∁UA)∩B=( )
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{a}$|=2$\sqrt{3}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$,$\overrightarrow{a}$⊥(3$\overrightarrow{a}$-$\overrightarrow{b}$),则|$\overrightarrow{b}$|等于( )
| A. | 6 | B. | 6$\sqrt{3}$ | C. | 12 | D. | 12$\sqrt{3}$ |
15.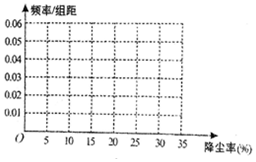 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器----雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过100次测试得到雾炮降尘率的频数分布表:| 降尘率(%)分组 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35] |
| 频数 | 10 | 15 | 10 | 25 | 20 | 15 | 5 |
(2)估计雾炮降尘率的平均数;
(3)若降尘率达到18%以上,则认定雾炮除尘有效,根据以上数据估计雾炮除尘有效的概率.
16.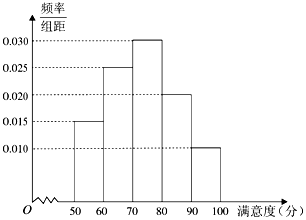 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
(Ⅰ)根据A公司的频率分布直方图,估计该公司满意度评分的中位数;
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:| 满意度 评分分组 | 频数 |
| [50,60) | 2 |
| [60,70) | 8 |
| [70,80) | 14 |
| [80,90) | 14 |
| [90,100] | 2 |
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
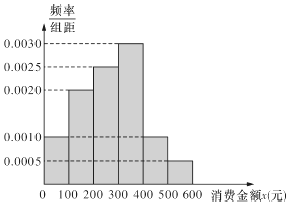 长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).
长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).