题目内容
(x+2)4展开式中含x2项的系数等于 .
考点:二项式定理的应用
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x2的幂指数等于1,求得r的值,即可求得展开式中的含x2项的系数.
解答:
解:(x+2)4展开式的通项公式为 Tr+1=C4r•x4-r•2r,
令4-r=2,求得 r=2,可得开式中含x2项的系数为 C42×22=24,
故答案为:24.
令4-r=2,求得 r=2,可得开式中含x2项的系数为 C42×22=24,
故答案为:24.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,则a+b的取值范围是( )
| A、[-1,1] | ||
B、[-
| ||
C、[0,
| ||
| D、[0,2] |
一组数据中每个数据都减去50构成一组新数据,则这组新数据的平均数是1.2,方差是4.4,则原来一组数的方差为( )
| A、3.2 | B、4.4 |
| C、4.8 | D、5.6 |
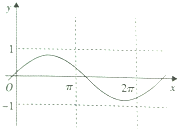
已知函数y=Asin(ωx+φ的图象如图所示,则该函数的解析式可能是( )

A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|