题目内容
已知实数a,b,c满足a+b+c=1,a2+b2+c2=1,则a+b的取值范围是( )
| A、[-1,1] | ||
B、[-
| ||
C、[0,
| ||
| D、[0,2] |
考点:柯西不等式
专题:计算题,不等式的解法及应用
分析:利用a+b+c=1,a2+b2+c2=1,可得a+b=1-c,ab=[(a+b)2-(a2+b2)]=c2-c,结合基本不等式,求出c的范围,即可求出a+b的取值范围.
解答:
解:∵a+b+c=1,a2+b2+c2=1,
∴a+b=1-c,ab=
[(a+b)2-(a2+b2)]=c2-c,
∵ab≤(
)2,
∴c2-c≤
,
∴-
≤c≤1,
∴0≤1-c≤
,
∴0≤a+b≤
,
故选:C.
∴a+b=1-c,ab=
| 1 |
| 2 |
∵ab≤(
| a+b |
| 2 |
∴c2-c≤
| (1-c)2 |
| 4 |
∴-
| 1 |
| 3 |
∴0≤1-c≤
| 4 |
| 3 |
∴0≤a+b≤
| 4 |
| 3 |
故选:C.
点评:本题考查a+b的取值范围,考查基本不等式的运用,比较基础.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
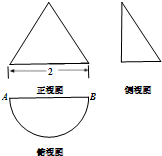 一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为
一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为