Question

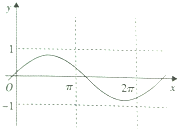
已知函数y=Asin（ωx+φ的图象如图所示，则该函数的解析式可能是（　　）

• A、y=

  4

  5

  sin（

  4

  5

  x+

  1

  5

  ）
• B、y=

  3

  2

  sin（2x+

  1

  5

  ）
• C、y=

  4

  5

  sin（

  4

  5

  x-

  1

  5

  ）
• D、y=

  4

  5

  sin（2x-

  1

  5

  ）

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由函数的图象的顶点坐标求出A，由周期求出ω，由特殊点的坐标求出φ的值，结合所给的选项，可得结论．

解答： 解：由函数的图象可得A∈（

1

2

，1），结合所给的选项可得A=

4

5

，故排除B．
∵函数的周期

2π

ω

＞2π，故有ω＜1，结合所给的选项可得ω=

4

5

，故排除D．
再根据

4

5

sinφ∈（0，

1

3

）可得sinφ∈（0，

1

2

），∴φ∈（0，

π

6

），故排除 C，
故选：A．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由特殊点的坐标求出φ的值，属于基础题．