题目内容
在一次知识竞赛中，有10名选手其成绩分布如下：
则这组数据的方差为 ．
| 成绩 | 4分 | 5分 | 6分 | 7分 | 8分 | 9分 | 10分 |
| 人数分布 | 2 | 0 | 1 | 3 | 2 | 1 | 1 |
考点：极差、方差与标准差
专题：概率与统计
分析：根据公式求出这组数据的平均数与方差．
解答：
解：这组数据的平均数是
=
=7.0，
方差是
s2=
[2×（4-7）2+（6-7）2+3×（7-7）2+2×（8-7）2+（9-7）2+（10-7）2]=3.4．
故答案为：3.4．
. |
| x |
| 4×2+6×1+7×3+8×2+9×1+10×1 |
| 10 |
方差是
s2=
| 1 |
| 10 |
故答案为：3.4．
点评：本题考查了求数据的平均数与方差的问题，解题时利用平均数与方差的公式进行计算即可．
练习册系列答案
相关题目
如图，PA垂直于以AB为直径的圆所在的平面，C为圆上异于A、B的任意一点，则有：①PA⊥BC；②BC⊥平面PAC；③AC⊥PB；④PC⊥BC．
上述关系正确的题号是（ ）
| A、①②③④ | B、①②④ |
| C、①②③ | D、①③④ |
已知m，n是不重合的两条直，α，β是不重合的两个平面．则以下结论正确的是（ ）
| A、若α⊥β，m⊥α，则m∥β |
| B、若m∥α，m⊥n，则n⊥α |
| C、若m⊥α，m⊥β，则α∥β |
| D、若m∥α，m?β，则α∥β |
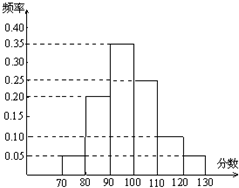某校高三文科分为四个班．高三数学调研测试后，随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人．抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120～130（包括120分但不包括130分）的频率为0.05，此分数段的人数为5人．f（x）=x2-6x+10，x∈[0，4]，此函数的最小值和最大值分别为（ ）
| A、无最大值也无最小值 |
| B、2，10 |
| C、有最小值1，无最大值 |
| D、1，10 |
已知焦点在x轴上的椭圆
+
2=1的离心率是e=
，则a的值为（ ）
| x2 |
| a2 |
| y |
| 9 |
| 1 |
| 2 |
A、2
| ||
B、
| ||
C、3
| ||
| D、12 |