题目内容
已知m,n是不重合的两条直,α,β是不重合的两个平面.则以下结论正确的是( )
| A、若α⊥β,m⊥α,则m∥β |
| B、若m∥α,m⊥n,则n⊥α |
| C、若m⊥α,m⊥β,则α∥β |
| D、若m∥α,m?β,则α∥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:∵m,n是不重合的两条直线,α,β是不重合的两个平面,
∴若α⊥β,m⊥α,则m∥β或m?β,故A错误;
若m∥α,m⊥n,则n与α相交、平行或n?α,故B错误;
若m⊥α,m⊥β,则由平面与平面平行的判定定理,得α∥β,故C正确;
若m∥α,m?β,则α与β平行或相交,故D错误.
故选:C.
∴若α⊥β,m⊥α,则m∥β或m?β,故A错误;
若m∥α,m⊥n,则n与α相交、平行或n?α,故B错误;
若m⊥α,m⊥β,则由平面与平面平行的判定定理,得α∥β,故C正确;
若m∥α,m?β,则α与β平行或相交,故D错误.
故选:C.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
阅读程序运行后,输出i=( )

| A、4 | B、5 | C、3 | D、7 |
已知直线l、m、n与平面α、β,给出下列四个命题:
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
| A、① | B、② | C、③ | D、③④ |
若实数x、y满足
,则S=2x+y的最大值为( )
|
| A、3 | B、2 | C、6 | D、7 |
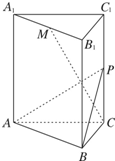 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在7.95米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在7.95米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.