题目内容
 如图,PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任意一点,则有:
如图,PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任意一点,则有:①PA⊥BC;②BC⊥平面PAC;③AC⊥PB;④PC⊥BC.
上述关系正确的题号是( )
| A、①②③④ | B、①②④ |
| C、①②③ | D、①③④ |
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:由PA⊥以AB为直径的圆所在的平面,可得A正确,由圆的性质可得AC⊥BC,可得B正确,由B及线面垂直的性质可得D正确.
解答:
解:由题意可得AC⊥BC,由PA⊥以AB为直径的圆所在的平面可知PA⊥BC,故①正确,
⇒BC⊥平面PAC,故②正确,
对于③假设AC⊥PB,结合选项②,可得AC⊥平面PBC,则AC⊥PC,又AC⊥PA,故③不正确,
利用直线与平面垂直的性质可得BC⊥PC,故④正确,
故选B.
|
对于③假设AC⊥PB,结合选项②,可得AC⊥平面PBC,则AC⊥PC,又AC⊥PA,故③不正确,
利用直线与平面垂直的性质可得BC⊥PC,故④正确,
故选B.
点评:本题主要考查了三垂线定理的运用,涉及到了“线面垂直”与“线线垂直”的转化,要求考生熟练掌握基本概念、基本定理.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
阅读程序运行后,输出i=( )

| A、4 | B、5 | C、3 | D、7 |
 在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.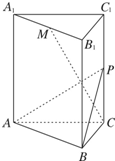 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2