题目内容
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列{
}的前200项和为( )
| 1 |
| anan-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:利用等差数列的通项公式可得an=n.于是
=
=
-
.利用“裂项求和”即可得出.
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:设等差数列{an}的公差为d,
∵a5=5,S5=15,
∴
,解得
∴an=1+(n-1)×1=n.
∴
=
=
-
.
∴数列{
}的前n项和Sn=(1-
)+(
-
)+…+(
-
)=
.
∴数列{
}的前200项和=
.
故选:A.
∵a5=5,S5=15,
∴
|
|
∴an=1+(n-1)×1=n.
∴
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{
| 1 |
| anan-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
∴数列{
| 1 |
| anan-1 |
| 200 |
| 201 |
故选:A.
点评:本题考查了等差数列的通项公式、“裂项求和”方法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以双曲线
-
=1的左顶点为焦点的抛物线的标准方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、y2=4x |
| B、y2=16x |
| C、y2=8x |
| D、y2=-8x |
若方程lnx+x-5=0在区间(a,b)(a,b∈Z,且b-a=1)上有一实根,则a的值为( )
| A、5 | B、4 | C、3 | D、2 |
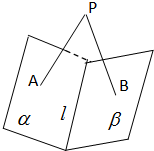 如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是
如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是